Algorithmic Thinking: A Problem-Based Introduction Homepage for the book Algorithmic Thinking: A Problem-Based Introduction

Solving a Segment Tree Problem, World of World of Warcraft

Hi everyone,

We haven’t done a segment tree problem on here yet. Not cool… let’s do one! Brush up on the segment tree material in Chapter 7 of the Algorithmic Thinking book, and let’s do this. We’re going to get things started in this post, and then follow-up with the remaining details in the next post. Between the two posts is a great time for you to finish up on your own before checking back on my solution.

The problem we’ll solve is the Wowow problem from the 2010 Canadian Computing Olympiad.

The Problem

A bunch of friends play a video game. Occasionally, new friends start playing. (Once they start playing, they never stop.) Each friend has a current rating. We’re asked to store and report on the friends’ ratings; we have to be able to add a friend with their initial rating, modify an existing friend’s rating, and report the friend whose ranked at a given position (first best, second best, etc.) in the ratings.

Input

The first line of input contains integer $n$ indicating the number of lines that will follow. $n$ is between $1$ and $1000000$.

Each of the next $n$ lines is an operation. There are three types of operations we must support:

  1. Add a friend. This operation is specified as the letter “N”, an integer $f$ indcating the new friend to add, and an integer $r$ giving the initial rating of this friend. $f$, the friend’s name, is between $1$ and $1000000$; $r$, the rating, is between $1$ and $100000000$. These bounds on friend names and ratings will be used throughout all operations.

  2. Modify a friend’s rating. This operation is specified as the letter “M”, an integer $f$ indcating the friend whose rating is to be modified, and an integer $r$ giving the new rating of this friend.

  3. Report friend. This operation is specified as the letter “Q” and an integer $k$. This is the only type of operation for which we produce output. Namely, we need to output the friend who right now has the $k$th best (i.e. highest) rating. If $k$ is $1$, we output the friend with the best rating; if $k$ is $2$, we output the friend with the second-best rating; and so on. $k$ is between $1$ and the number of friends that currently have ratings. For example, if we’ve had five “N” operations to this point, then $k$ would be between $1$ and $5$.

It’s guaranteed that no two friends ever have the same rating.

Output

Output the correct friend for each “Q” operation.

Example

Let’s go through a little test case. Here it is:

8
N 3 700
N 1 500
Q 2
N 7 1000
Q 2
M 3 45000
Q 2
Q 1

The correct output for this test case is therefore:

1
3
7
3

Why Segment Trees?

Focus on the “Q” operations for a sec. Suppose that we weren’t using trees and had to find the 5120th-highest rating in a huge list of friends and ratings. How would we do it? Slowly, I’d bet! For example, we could sort the whole list and then return the friend at position 5120. But that would be way too slow. We need a faster way to do this. If we could manage to use a segment tree, with its logarithmic height, then we’d be in great shape.

In Chapter 7, I discussed telltales for when a segment tree might be useful. One of those signs is that we can solve a query by using what we know about the subqueries. Just like for the Range Minimum Query that we solved there, we’ll be able to efficiently keep a segment tree updated here, too.

I think a natural first approach is to store the names of the friends (their integer numbers) in the leaves of the segment tree, similar to what we did in the two examples in Chapter 7. But suppose we’re looking at the root of such a segment tree, and we want to know which side of the tree (left or right) has the $k$th-highest rating. We might know how many friends are in each half, but we won’t know anything about how many of those friends have higher or lower ratings than what we’re looking for.

No — rather than a segment tree on the friends’ names, we’ll use a segment tree on the ratings. IMO this is the single most important insight for solving this problem, so let’s study a sample segment tree to make sure we’ve got this.

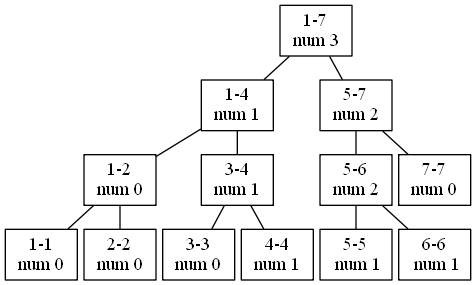
Segment tree on the ratings from 1 to 7. Ratings 4, 5, and 6 are present.

Each interval keeps track of the number of ratings that are present in that interval. For example, the 1-7 interval has 3 ratings in it, the 1-4 interval has 1, and the 1-2 interval has 0. Alternatively, you can think of this as keeping track of the sum of a bunch of 1s and 0s, where each 1 means that a rating is present and each 0 means that a rating is not.

OK – so how can we use this thing? Let’s suppose we want to find the second-highest rating in here. Where is it? Is it in the left subtree of the root? Is it in the right subtree of the root? If we could figure this out, then we could move down one level in the tree and repeat this process.

The right subtree, interval 5-7, has 2 ratings in it. And they are the highest 2! So our second-highest rating is guaranteed to be there. We can completely ignore the 1-4 interval and focus on the 5-7 interval.

Now the right subtree of 5-7, interval 7-7, has no ratings in it, so our second-highest rating can’t be in there. It has to be in the 5-6 subtree.

Is it in the right subtree of 5-6? Well, no: there’s only 1 rating in there, the highest one, and we’re looking for the second-highest. So the rating we want must be in the 5-5 subtree.

Asking for the second-highest rating in the 5-5 subtree wouldn’t make any sense at all, because 5-5 has only one rating. Fortunately, that’s not what we’re going to do. We threw away 1 high rating from the 6-6 subtree, so now actually we want the highest rating in the 5-5 subtree (which is the second-highest rating overall).

Let’s do one more example. Suppose we want the third-highest rating this time. 5-7 has 2 ratings in it, so what we want isn’t in there. Instead, it’s in the 1-4 subtree. We just eliminated 2 high ratings, so in the 1-4 subtree we’re looking for the $3-2=1$st-highest rating, because that will be the 3rd-highest rating overall. Follow this process through, and you’ll find that this rating is 4.

Some Initial Code

Let’s get on to some code. As I noted at the beginning, this isn’t going to fully solve the problem. But it’s a start, and I wanted to give everyone the fun (and frustration… maybe a little of that… it’s healthy!) of thinking through the rest. After the code, we’ll talk about what this code does well and what it doesn’t.

Here’s the code.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_RATING 1000000

typedef struct segtree_node {
  int left, right;
  int num_ratings; // Number of people with ratings in the range left..right
} segtree_node;

void init_segtree(segtree_node segtree[], int node,
                  int left, int right) {
  int mid;
  segtree[node].left = left;
  segtree[node].right = right;
  if (left == right)
    return;
  mid = (left + right) / 2;
  init_segtree(segtree, node * 2, left, mid);
  init_segtree(segtree, node * 2 + 1, mid + 1, right);
}

int query_segtree(segtree_node segtree[], int node, int k) {
  int in_right;

  if (segtree[node].left == segtree[node].right)
    return segtree[node].left;

  in_right = segtree[node * 2 + 1].num_ratings;
  if (in_right >= k)
    return query_segtree(segtree, node * 2 + 1, k);
  else
    return query_segtree(segtree, node * 2, k - in_right);
}

void bump_rating_segtree(segtree_node segtree[], int node, int rating,
                         int up_down) {
  int left_max_index;

  segtree[node].num_ratings += up_down;

  if (segtree[node].left == segtree[node].right)
    return;

  left_max_index = segtree[node * 2].right;
  if (rating <= left_max_index)
    bump_rating_segtree(segtree, node * 2, rating, up_down);
  else
    bump_rating_segtree(segtree, node * 2 + 1, rating, up_down);
}

int main(void) {
  static segtree_node segtree[MAX_RATING * 4 + 1];
  int n, i, friend, rating, k;
  char code;

  init_segtree(segtree, 1, 1, MAX_RATING);

  scanf("%d", &n);
  for (i = 0; i < n; i++) {
    scanf(" %c", &code);
    if (code == 'N') { // New friend
      scanf("%d%d", &friend, &rating);
      bump_rating_segtree(segtree, 1, rating, 1);
    } else if (code == 'M') { // Modify friend rating
      scanf("%d%d", &friend, &rating);
      printf(":( [TODO] modify friend %d to have rating %d\n", friend, rating);
    } else { // Query kth highest rating
      scanf("%d", &k);
      // Wrong: reports the rating, not the friend with that rating
      printf("%d\n", query_segtree(segtree, 1, k));
    }
  }
  return 0;
}

We have a standard segment tree node here (7), just like those in the book. In addition to the left and right indicators, we keep track of the number of ratings in this range.

We initialize the segment tree segments in the usual way (12-22) – nothing new here.

To query the segment tree (24), we carry out the tree algorithm that we detailed above. First, we check whether we’re in the base case of a tree with a single node (27). If we are, then that’s the rating we want (28). Otherwise, we look at the number of nodes in the right subtree (30). If our desired rating is in those big ratings (31), then we recurse on that subtree searching for the same rating as before (because we’re not getting rid of any high ratings by ignoring the left subtree). Otherwise, the ratings in the right subtree are too big, so we search instead in the left subtree (34). Here, we subtract the number of ratings in the right subtree, because ignoring those high ratings brings us that much closer to finding the rating that we want.

The final helper function I’ve got here is bump_rating_segtree (37). It changes the provided rating by up_down, and updates all of rating’s ancestors accordingly. If up_down is 1, then it will have the effect of increasing the provided rating from 0 (not currently a rating) to 1 (an active rating now!).

Now let’s see what this tree and our helper functions can help us do in terms of the three types of operations we need to support.

So, two problems: we don’t know how to go from a friend’s name to their rating, and we don’t know how to go from a rating to a friend’s name.

Erm, well, three problems. The third hides in the maximum number of ratings (5) that we support, which is currently 1000000. Only 1000000? From the problem description, we know that we need to support up to 100000000 ratings. You might try cranking it up just like this:

#define MAX_RATING 100000000

But it turns out that this uses more memory than the problem allows. Such a segment tree would require $4*100000000=400000000$ nodes. The problem only allows us to use 256MB. 400 million nodes, only 256 million bytes of memory? Not going to work. We need a way to use fewer nodes. And the way to do that is to use the fact that there are a maximum of only 1000000 operations. Each operation can refer to at most one rating, right? So there can be at most 1000000 active ratings at any one time! We have to find a way to store information only about those ratings.

And Now Your Turn…

That’s where I’ll leave off for this post. Can you finish up the code and fully solve this problem? Go for it! And check back on Dec 14 if you want to join me to the conclusion.

And finally, Just FYI, I maintain a very low-traffic newsletter where I send occasional updates related to the book and what’s going on here on the blog. Please see my Contact and Newsletter page if you’re interested. Thanks!

Written on December 7th, 2020 by Daniel Zingaro
Feel free to share!

You may also enjoy: