Algorithmic Thinking: A Problem-Based Introduction Homepage for the book Algorithmic Thinking: A Problem-Based Introduction

Solving a Nice Segment Tree Problem, Snjeguljica

Hello!

Thank you to everyone who has been providing feedback on my Algorithmic Thinking book. While different chapters resonate most with different people, one of the things that keeps coming up about the segment trees material in Chapter 7 is that not many other books cover this ground. That’s too bad because, as you know from Chapter 7, segment trees are deceptively powerful data structures. And once you have the code and understanding from Chapter 7, you can use them yourself to solve new problems. I’m glad that I included them in the book. In future writing, I will try to include even more examples of powerful data structures and algorithms that are not often found in other books.

Wanna solve another problem using segment trees? Let’s do it!

The problem we’ll solve this time is the Snjeguljica problem from the 2012 Croatian Open Competition in Informatics.

The Problem

There are $n$ people in a row. Each person has a unique height between $1$ and $n$. (For example, for five people, their heights could be 2 4 1 3 5; but there can’t be repeats, so 2 4 2 3 5 is not allowed.) For this reason, each height between $1$ and $n$ is going to be used exactly once.

The people in the row start off in some arbitrary order. We say that the first person is at location 1, the second person is at location 2, and so on.

Alright. So we have the people there in the row – and then two kinds of operations can happen:

  1. The first is that the two people in specified locations switch places. For example, we might have to swap the locations of the people at locations 3 and 1.

  2. The second is that we ask whether the people whose heights are between heights $a$ and $b$ are standing consecutively together with no one else. We’re not requiring that these people are in order of height, just that they’re grouped together with no one else in the group. For example, if the heights in the row were 2 4 1 3 5, and we wanted to know whether the people whose heights from 2 to 5 are consecutive, then the answer would be “no” because the person with height 1 is in the way. But if the heights were 1 4 2 3 5, then the answer would be “yes” because 4 2 3 5 are exactly the heights that we need. That is, the answer is “yes” exactly when you can find a starting point and ending point that captures exactly the heights that you need, with no one else allowed in there.

We have to be able to efficiently carry out both of these kinds of operations.

Input

The first line of input contains integer $n$ indicating the number of people in the row, and integer $m$ indicating the number of operations. Each of these integers is between $2$ and $200000$.

The next line contains $n$ space-separated positive integers between $1$ and $n$, each exactly once, representing the heights of the people in the row.

Each of the next $m$ lines is an operation:

  1. Swap People. This operation is specified as the number 1, the location of the first person, and the location of the second person.

  2. Are these people standing together? This operation is specified as the number 2, the height $a$, and the height $b$. It’s guaranteed that $a \le b$. This is the only type of operation for which we produce output. Namely, we need to output YES if all people with heights $a, a+1, a+2, \ldots, b$ are consecutive in the row in some order, or NO if not.

Output

Output the correct YES/NO answer for each 2 operation.

Examples

Let’s start with the first test case provided in the problem description. Here it is:

5 3
2 4 1 3 5
2 2 5
1 3 1
2 2 5

The correct output for this test case is therefore:

NO
YES

Now let’s work through the second test case provided in the problem description. I’m going to throw in some analysis along the way, which will help motivate why segment trees are useful for this problem and how we’ll ultimately use them. Here’s the test case:

7 7
4 7 3 5 1 2 6
2 1 7
1 3 7
2 4 6
2 4 7
2 1 4
1 1 4
2 1 4

The correct output for this test case is therefore:

YES
NO
YES
NO
YES

Extrapolating from this test case, here’s the rule that we’ll use for each 2 operation: if we care about $n$ people and the relevant subrange has exactly $n$ people in it, we answer YES; otherwise, we answer NO.

Why Segment Trees?

Suppose we didn’t use segment trees for this problem. Where would we run into trouble? Well, handling the 1 operations would be no problem – just perform the swap for each one. But the 2 operations? Those would hammer us. For each one, we’d have to find the minimum relevant location and the maximum relevant location, and this may require a full scan of our row array. That would be a linear time operation for each 2 operation. No good!

As you learned in Chapter 7, the key to solve any segment tree problem is to figure out what we need to store in each node. Here, we need to store the minimum relevant index and the maximum relevant index.

Let’s look at the segment tree for the 4 7 3 5 1 2 6 heights we studied earlier. Here it is:

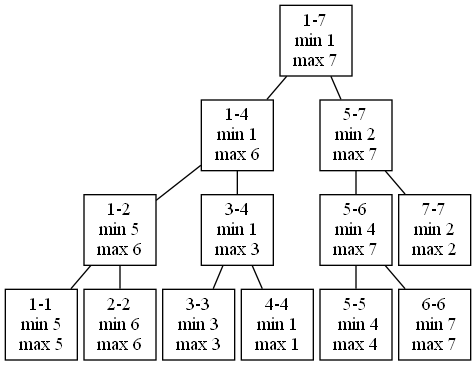
Segment tree on heights from 1 to 7.

In each node, “min” refers to the minimum relevant location and “max” refers to the maximum relevant location.

For any node whose left and right indices are the same, min and max are going to be equal. For example, for the 1-1 node, both min and max are 5. Why 5? Because location 5 is where the person of height 1 is. Hmm, so when we’re building the tree, we’re going to need a way to go from a height to the location of that height in the row. Keep that in mind as you soon study the code!

For any other node in the tree, the min and max values are calculated from the child nodes. As per Chapter 7, this is the key thing that allows a segment tree solution to work. For example, consider the 1-4 node. The minimum relevant location is 1. Why? Because that’s the minimum of the min values of its children! The maximum relevant location is 6. Why? Because that’s the maximum of the max values of its children!

The Code

Now, the code! I’ve based it heavily on the segment tree code that we used to solve the Two Sum problem in Chapter 7 of Algorithmic Thinking. A thank-you to Xing Lyu, whose code helped me quickly fix a bug and further streamline my code!

I want everyone to be able to benefit from my work here on the blog; even if you don’t have the book, you can download the code for free here.

I’d also like to highlight that we previously solved Another Segment Tree Problem right here on this blog; the code there shares some ideas with our code here as well.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_HEIGHTS 200000
#define REALLY_SMALL -1E6
#define REALLY_BIG 1E6

typedef struct segtree_node {
  int left, right;
  int min_location, max_location;
} segtree_node;

typedef struct node_info {
  int min_location, max_location;
} node_info;

void init_segtree(segtree_node segtree[], int node,
                  int left, int right) {
  int mid;
  segtree[node].left = left;
  segtree[node].right = right;
  if (left == right)
    return;
  mid = (left + right) / 2;
  init_segtree(segtree, node * 2, left, mid);
  init_segtree(segtree, node * 2 + 1, mid + 1, right);
}

int min(int v1, int v2) {
  if (v1 < v2)
    return v1;
  else
    return v2;
}

int max(int v1, int v2) {
  if (v1 > v2)
    return v1;
  else
    return v2;
}

void swap(int *a, int *b) {
  int temp = *a;
  *a = *b;
  *b = temp;
}

node_info fill_segtree(segtree_node segtree[], int node,
                       int locations[]) {
  node_info left_info, right_info;

  if (segtree[node].left == segtree[node].right) {
    segtree[node].min_location = locations[segtree[node].left];
    segtree[node].max_location = locations[segtree[node].left];
    return (node_info){segtree[node].min_location, segtree[node].max_location};
  }

  left_info = fill_segtree(segtree, node * 2, locations);
  right_info = fill_segtree(segtree, node * 2 + 1, locations);

  segtree[node].min_location = min(left_info.min_location,
                                   right_info.min_location);
  segtree[node].max_location = max(left_info.max_location,
                                   right_info.max_location);
  return (node_info){segtree[node].min_location, segtree[node].max_location};
}

node_info query_segtree(segtree_node segtree[], int node,
                        int left, int right) {
  node_info left_info, right_info;

  if (right < segtree[node].left || left > segtree[node].right)
    return (node_info){REALLY_BIG, REALLY_SMALL};

  if (left <= segtree[node].left && segtree[node].right <= right)
    return (node_info) {segtree[node].min_location, segtree[node].max_location};

  left_info = query_segtree(segtree, node * 2, left, right);
  right_info = query_segtree(segtree, node * 2 + 1, left, right);
  return (node_info) {min(left_info.min_location, right_info.min_location),
                      max(left_info.max_location, right_info.max_location)};
}

node_info update_segtree(segtree_node segtree[], int node,
                         int locations[], int index) {
  segtree_node left_node, right_node;
  node_info left_info, right_info;

  if (segtree[node].left == segtree[node].right) {
    segtree[node].min_location = locations[index];
    segtree[node].max_location = locations[index];
    return (node_info) {segtree[node].min_location, segtree[node].max_location};
  }

  left_node = segtree[node * 2];
  right_node = segtree[node * 2 + 1];

  if (index <= left_node.right ) {
    left_info = update_segtree(segtree, node * 2, locations, index);
    right_info = (node_info){right_node.min_location, right_node.max_location};
  } else {
    right_info = update_segtree(segtree, node * 2 + 1, locations, index);
    left_info = (node_info){left_node.min_location, left_node.max_location};
  }

  segtree[node].min_location = min(left_info.min_location,
                                   right_info.min_location);
  segtree[node].max_location = max(left_info.max_location,
                                   right_info.max_location);

  return (node_info) {segtree[node].min_location, segtree[node].max_location};
}

int main(void) {
  static int locations[MAX_HEIGHTS + 1];
  static int heights[MAX_HEIGHTS + 1];

  static segtree_node segtree[MAX_HEIGHTS * 4 + 1];
  int num_heights, num_ops, i, next_height, op, x, y;
  int height1, height2, subsequence_length;
  node_info result;

  scanf("%d%d", &num_heights, &num_ops);
  for (i = 1; i <= num_heights; i++) {
    scanf("%d", &next_height);
    locations[next_height] = i;
    heights[i] = next_height;
  }
  init_segtree(segtree, 1, 1, num_heights);
  fill_segtree(segtree, 1, locations);

  for (i = 0; i < num_ops; i++) {
    scanf("%d%d%d", &op, &x, &y);

    if (op == 1) {
      height1 = heights[x];
      height2 = heights[y];
      swap(&locations[height1], &locations[height2]);
      swap(&heights[x], &heights[y]);
      update_segtree(segtree, 1, locations, height1);
      update_segtree(segtree, 1, locations, height2);
    } else {
      result = query_segtree(segtree, 1, x, y);
      subsequence_length = result.max_location - result.min_location + 1;
      if (subsequence_length == y - x + 1)
        printf("YES\n");
      else
        printf("NO\n");
    }
  }
  return 0;
}

We have a standard segment tree node here (9), just like those in the book. In addition to the left and right indicators, we keep track of both the relevant minimum and relevant maximum locations.

We initialize the segment tree segments as we always do (18-28) – nothing new here. In fact, there’s not much new about the segment tree code in general, so let’s focus on what’s going on in the main function (116).

The heights array (118) is our row of heights; for example, [4, 7, 3, 5, 1, 2, 6]. You feed it a location and it gives you the height. The name of the array tells you what you get when you index it (i.e. a height).

That heights array is useful to have, but also remember that to build the segment tree we need to know which location is currently being used to store a given height. For example, to correspond with the array [4, 7, 3, 5, 1, 2, 6], we need this array: [5, 6, 3, 1, 4, 7, 2]. This tells us that height 1 is at location 5, height 2 is at location 6, and so on. This array, where you feed it a height and it gives you the location, is locations (117). The name of the array tells you what you get when you index it (i.e. a location). And notice how crucial this locations array is in filling the segment tree (55-56).

OK. Now we’re ready to talk about the two kinds of operations:

In Closing

You know the heights and locations arrays that we used here? You can think of them as inverted versions of the same data: one goes from locations to heights, and the other goes the other way from heights to locations. It’s surprising how often we need to store the same data in different ways to facilitate different types of access. This same idea also came up back when we solved the other segment tree problem on this blog. If your data lets you go in one direction but you need to go in the opposite direction, chances are that you need to add another array or structure that lets you access your data in a different way.

Thank you, everyone. Until next time!

Written on April 12th, 2022 by Daniel Zingaro
Feel free to share!

You may also enjoy: